A seamrix (từ động từ Latinh trahere "kéo, kéo"; số nhiều: máy kéo ) là đường cong mà vật thể di chuyển, bên dưới ảnh hưởng của ma sát, khi được kéo trên mặt phẳng nằm ngang bởi một đoạn thẳng gắn với điểm máy kéo (kéo) di chuyển theo một góc vuông với đường ban đầu giữa vật và dụng cụ kéo với tốc độ vô hạn. Do đó, nó là một đường cong của sự theo đuổi. Nó được Claude Perrault giới thiệu lần đầu tiên vào năm 1670, và sau đó được nghiên cứu bởi Isaac Newton (1676) và Christiaan Huygens (1692). [ cần trích dẫn ]
Đạo hàm toán học [ chỉnh sửa ]
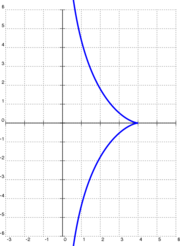
Giả sử đối tượng được đặt tại ( a 0) (hoặc (4.0) trong ví dụ hiển thị ở bên phải) và trình kéo ở gốc, vì vậy a là độ dài của chỉ kéo (4 trong ví dụ ở bên phải). Sau đó, bộ kéo bắt đầu di chuyển dọc theo trục y theo hướng tích cực. Tại mọi thời điểm, luồng sẽ tiếp xúc với đường cong y = y ( x ) được mô tả bởi đối tượng, do đó nó được xác định hoàn toàn bởi sự chuyển động của người kéo. Về mặt toán học, chuyển động sẽ được mô tả sau đó bằng phương trình vi phân
với điều kiện ban đầu y ( a ) = 0 có giải pháp là
Thuật ngữ đầu tiên của giải pháp này cũng có thể được viết
trong đó arsech là chức năng bảo mật hyperbolic nghịch đảo .
Nhánh âm biểu thị trường hợp người kéo di chuyển theo hướng tiêu cực từ gốc. Cả hai nhánh đều thuộc về máy kéo, gặp nhau tại điểm cusp ( a 0) .
Cơ sở của máy kéo [ chỉnh sửa ]
Thuộc tính thiết yếu của máy kéo là khoảng cách giữa một điểm P trên đường cong và giao điểm của đường tiếp tuyến tại P với tiệm cận của đường cong.
Máy kéo có thể được xem xét theo nhiều cách:
- Đây là vị trí trung tâm của một cuộn xoắn ốc hyperbol (không trượt) trên một đường thẳng.
- Sự liên quan của chức năng dây xích, mô tả một chuỗi hoàn toàn linh hoạt, không đàn hồi, gắn liền với hai điểm chịu một trường hấp dẫn. Dây xích có phương trình y ( x ) = a cosh x / a . quỹ đạo được xác định bởi giữa trục sau của ô tô được kéo bởi một sợi dây với tốc độ không đổi và có hướng không đổi (ban đầu vuông góc với xe).

Hàm này thừa nhận một đường ngang tiệm cận. Đường cong đối xứng với y -axis. Bán kính cong là r = a cot x / y .
Một hàm ý tuyệt vời mà máy kéo có được là nghiên cứu về bề mặt cách mạng của nó xung quanh tiệm cận của nó: giả hành. Được nghiên cứu bởi Eugenio Beltrami vào năm 1868, [ cần trích dẫn ] như một bề mặt của độ cong Gaussian âm liên tục, hình cầu giả là một mô hình địa phương của hình học phi Euclide. Ý tưởng đã được Kasner và Newman tiếp tục thực hiện trong cuốn sách của họ Toán học và Trí tưởng tượng [ trích dẫn cần thiết ] tạo ra máy kéo.
Thuộc tính [ chỉnh sửa ]

- Do cách xác định hình học, máy kéo có đặc tính là đoạn tiếp tuyến của nó, giữa tiệm cận và điểm tiếp tuyến, đã chiều dài không đổi a .
- Độ dài cung của một nhánh nằm trong khoảng x = x 1 và x = x 2 là a ln x 1 / x 2 .
- và tiệm cận của nó là π a 2 / 2 có thể được tìm thấy bằng cách sử dụng tích hợp hoặc định lý Mamikon.
- Đường bao của các quy tắc của máy quét (đó là là, sự phát triển của máy kéo) là đường cong dây xích (hoặc ) được đưa ra bởi y = a cosh x / [19659082] a .
- Bề mặt của cuộc cách mạng được tạo ra bằng cách quay vòng một máy kéo về tiệm cận của nó là một giả hành.
Ứng dụng thực tế [ chỉnh sửa ]
Vào năm 1927, P. G. A. H. Voigt đã cấp bằng sáng chế cho thiết kế loa sừng giả định rằng một mặt sóng truyền qua sừng là hình cầu có bán kính không đổi. Ý tưởng là để giảm thiểu sự biến dạng gây ra bởi sự phản xạ bên trong của âm thanh trong sừng. Hình dạng kết quả là bề mặt của cuộc cách mạng của máy kéo. [1]
Một ứng dụng quan trọng là trong công nghệ tạo hình cho kim loại tấm. Cụ thể, một cấu hình máy kéo được sử dụng cho góc của khuôn mà kim loại tấm bị uốn cong trong khi vẽ sâu. [2]
Thiết kế ròng rọc vành đai răng mang lại hiệu quả cải thiện cho việc truyền năng lượng cơ học bằng cách sử dụng một hình dạng dây xích cho răng của nó. [3] Hình dạng này giảm thiểu ma sát của răng vành đai gắn với ròng rọc, bởi vì các răng di chuyển tham gia và nhả ra với tiếp xúc trượt tối thiểu. Thiết kế vành đai thời gian ban đầu sử dụng hình dạng răng hình thang hoặc hình tròn đơn giản hơn, gây ra trượt và ma sát đáng kể.
Máy vẽ [ chỉnh sửa ]
- Vào tháng 10 năm 16 tháng 11 năm 1692, Christiaan Huygens đã mô tả ba máy vẽ máy kéo. [ cần trích dẫn ]
- Năm 1693, Gottfried Wilhelm Leibniz đã nghĩ ra một "cỗ máy kéo vạn năng", theo lý thuyết, có thể tích hợp bất kỳ phương trình vi phân nào. [4] Khái niệm này là một cơ chế tính toán tương tự thực hiện nguyên lý lực kéo. Thiết bị này không thực tế để chế tạo theo công nghệ của thời Leibniz và không bao giờ được nhận ra.
- Năm 1706, John Perks đã chế tạo một máy kéo để thực hiện phương pháp bậc hai. [5] 1729 Johann Poleni đã chế tạo một thiết bị lực kéo cho phép rút ra các chức năng logarit. [6]
Lịch sử của tất cả các máy này có thể được nhìn thấy trong một bài viết của HJM Bos [7]
Xem thêm [ chỉnh sửa ]
Tài liệu tham khảo [ chỉnh sửa ]
Liên kết ngoài [ chỉnh sửa ]
| Wikimedia Commons có phương tiện liên quan đến Tractrix |
visit site
site


No comments:
Post a Comment